redis的zset和set都使用跳表实现。跳表简单地说，就是在链表上构造多级索引，以加速查找，是用空间换时间。它比红黑树实现更简单，不需要耗费大量的精力维护树的平衡。跳表的各个节点是有顺序的，可以进行范围查询。
本文将分析跳表的构成、插入、删除等操作，并使用go实现。
1. 跳表结构
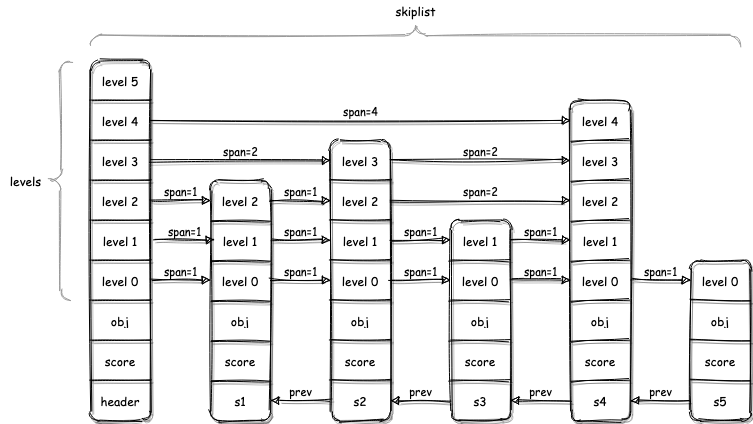
上图就是一个包含5个节点的跳表结构。跳表的结构包含一个又一个的节点，和header节点。header节点是查询的起始点。跳表定义如下，包含头结点、尾节点、长度以及跳表的索引层数。
// skiplist 持有一个跳表的完整数据
type skiplist struct {
// header和tail表示跳表的头结点和尾节点
header, tail *skiplistNode
// length 表示跳表的长度
length int
// level 表示该跳表索引的层数
level int
}
从上面跳表的定义看不出什么，跳表每个节点的定义就有很多东西了。
// skiplistLevel 表示skiplist每一节点在每一层持有的数据结构
type skiplistLevel struct {
// 该层节点的下一个节点，redis使用forward
next *skiplistNode
// 该层节点到下一节点中间间隔的跳数
span int
}
// skiplistNode 表示skiplist的每一个节点
type skiplistNode struct {
// robj 代表该节点的数据
robj interface{}
// score 表示该节点的分数，以便排序
score float64
// prev 表示该节点的上一节点，redis 中使用backward
prev *skiplistNode
// levels 表示该节点在每一层索引中到下一节点的信息
levels []skiplistLevel
}
每一个节点中持有数据robj、该数据的分数score用来排序、上一节点的指针prev以便于反向遍历、各层索引信息levels。每一层的索引信息skiplistlevel包括该层索引中该节点指向的下一个节点的指针next、该节点到下一节点的间隔span。例如上图中，节点s2在第三层索引的下一节点是s4，而在第二层索引的下一节点是s3，而且间隔span分别是2和1。
每个节点的索引层数通过随机数生成，redis设计的思路：使用第n级索引是使用第n-1级索引概率的1/4，最多使用32级索引，如果真用到了32级索引，这个跳表所持有的数据也是巨大的，因此不用担心索引不够用。
func randomLevel() int {
var level = 1
// SKIPLIST_P = 0.25
for rand.Float64() < SKIPLIST_P {
level ++
}
if level < SKIPLIST_MAXLEVEL {
return level
}
return SKIPLIST_MAXLEVEL
}
跳表按照score和robj从小到大进行排序，因此它的各个节点是有序的，可以进行范围查找。
// compareObj 如果obj1>obj2，返回true
func compareObj(obj1, obj2 interface{}) bool {
var t1, t2 reflect.Type
t1 = reflect.TypeOf(obj1)
t2 = reflect.TypeOf(obj2)
if t1.Kind() != t2.Kind() {
compareObj(fmt.Sprint(obj1), fmt.Sprint(obj2))
}
var v1, v2 reflect.Value
v1 = reflect.ValueOf(obj1)
v2 = reflect.ValueOf(obj2)
switch t1.Kind() {
case reflect.Int:
return v1.Int() > v2.Int()
case reflect.Float64, reflect.Float32:
return v1.Float() > v2.Float()
case reflect.String:
return v1.String() > v2.String()
}
return compareObj(fmt.Sprint(obj1), fmt.Sprint(obj2))
}
2. 节点的插入
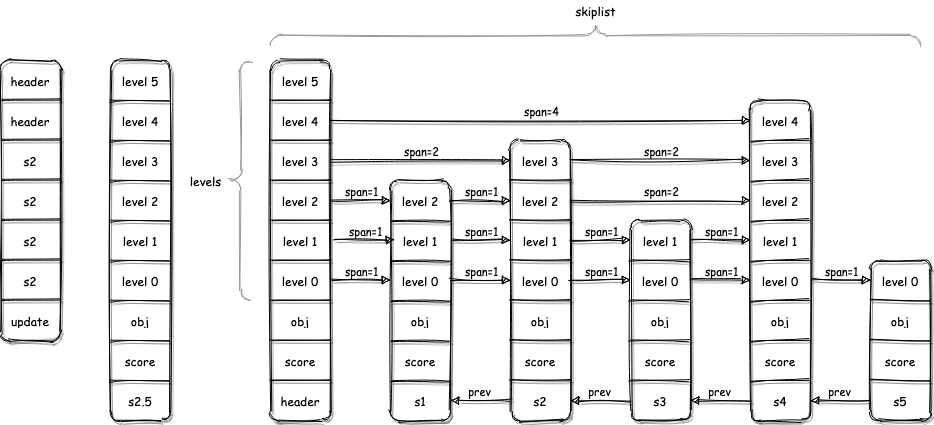
在链表中如果要插入一个节点S，需要找到在链表中比S小的最大节点F，把S挂在F节点后面。那么在跳表中也是这样的套路，只不过更复杂一些。下面分几步将上图中s2.5节点挂在s2后面，已知s2.5的score或者obj比s2的score或obj要大，但是小于s3。
2.1. 查找比s2.5小的最大节点
在插入新节点之前，需要找到新节点可以插入的位置，就需要找出每一层索引中新节点的前一节点，这里就是比s2.5小的最大节点。跳表有五层索引，表示为0-4。跳表的起点是header，因此查找节点时需要从header的level 4开始进行，表示为header.levels[4]。代码中使用update[i]表示第i层索引中比s2.5小的最大节点指针。注意下面的代码还有一个rank数组，rank[i]就表示第i层索引中，update[i]节点到header的span，下面注意它是怎么增加的。
- 从header.levels[4]开始向右遍历，此时rank[4]=0；header.levels[4]下一节点是s4比s2.5大，因此该层索引中s2.5的上一节点就是header，即update[4]=header，接下来向下进入第3层索引，即header.levels[3]
- 第3层索引中，初始rank[3] =rank[4]=0，向右遍历搜索到header的下一节点s2。s2就是这一层s2.5需要插入的位置的前一节点，因此update[3]=s2，rank[3]=rank[3]+header.levels[3].span=2，然后向下进入s2.levels[2]
- 依次遍历第2、1、0层索引，路径为s2.levels[2]->s2.levels[1]->s2.levels[0]，求得update[2]=update[1]=update[0]=s2，rank[2]=rank[1]=rank[0]=rank[3]=2。到这里，通过走楼梯的方式将s2.5需要插入的位置全找出来了
x = sl.header
for i := sl.level-1; i >= 0; i -- {
if i == sl.level-1 {
rank[i] = 0
} else {
rank[i] = rank[i+1]
}
// 寻找比score和robj小的最近节点
for x.levels[i].next != nil && (x.levels[i].next.score < score ||
(x.levels[i].next.score == score && compareObj(robj, x.levels[i].next.robj))) {
rank[i] += x.levels[i].span
x = x.levels[i].next
}
update[i] = x
}
2.2. 插入节点s2.5
现在有了update数组表示各层索引中s2.5的上一节点位置，以及rank数组表示update各节点到header的距离，就可以进行s2.5的插入了。
var level = randomLevel()
// 代码1
if level > sl.level {
for i := sl.level; i < level; i ++ {
rank[i] = 0
update[i] = sl.header
update[i].levels[i].span = sl.length
}
sl.level = level
}
//-----
x = createSkiplistNode(level, score, robj)
// 代码2
for i := 0; i < level; i ++ {
x.levels[i].next = update[i].levels[i].next
update[i].levels[i].next = x
x.levels[i].span = update[i].levels[i].span - (rank[0]-rank[i])
update[i].levels[i].span = rank[0] - rank[1] + 1
}
// -----
// 代码3
for i := level-1; i < sl.level; i ++ {
update[i].levels[i].span ++
}
//-----
// 如果当前节点是插入的第一个节点，它的prev是nil
if update[0] == sl.header {
x.prev = nil
} else {
x.prev = update[0]
}
if x.levels[0].next != nil {
x.levels[0].next.prev = x
} else {
sl.tail = x
}
sl.length ++
-
首先通过随机算法randomLevel()获取该节点的索引层数
-
现在有两种情况：level比跳表原来的层数sl.level要大或者level小于等于sl.level
-
- 首先处理level>sl.level的情况（代码1）。高于sl.level小于level的索引i中，s2.5的前一节点就直接是header，因此设置update[i]=header，同时rank[i]=0。header.levels[i].span设置为跳表的长度。设置sl.level=level。
- 现在只有level<=sl.level的情况了（代码2）。当索引i<level时，直接将s2.5挂在update[i].levels[i]的后面，并更新update[i].levels[i]和s2.5.levels[i]的span
- 而在level<=sl.level的情况（代码3），当level<=索引i<sl.level时，直接把update节点的span加一。因为此时新节点的索引层数level比跳表的层数少，那么新节点的插入对于比level高的索引节点来说就是将其与后面节点的距离增加了一个单位。
-
处理s2.5的prev指针，由上面的图也可以知道prev指针和第0层的索引是反向的，但是并不会指向header。这里我认为是为了方便反向遍历，如果s1.prev指向header，在反向遍历时需要加一层header的判断。
-
处理跳表的tail指针，如果插入的节点在最后，则重新设置tail
-
更新跳表长度
3. 删除节点
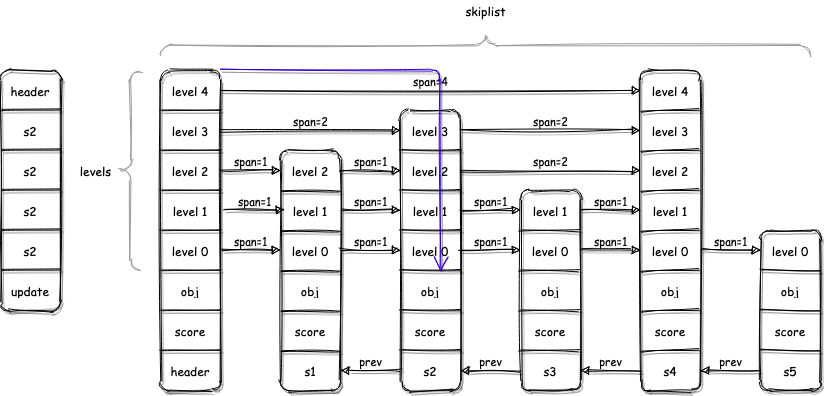
上图中，如果想删除s3节点，需要两步：找到s3节点在各层索引处的上一节点；删除s3节点。
3.2. 查找比s3小的最大节点
查找的算法依旧是从header的最高层索引开始下楼梯，并使用update数组保存每一层索引中s3的前一个节点。
在上图中：
- 从header.levels[4]开始向右遍历，找不到其他的节点小于s3，因此向下遍历header.levels[3]，第4层的最大节点是header，即update[4]=header
- 依次类推，update[3]=s2，update[2]=s2，update[1]=update[0]=s2，遍历路径见图中的蓝色箭头。
// 查找最近节点
x = sl.header
for i := sl.level-1; i >= 0; i -- {
for x.levels[i].next != nil && (x.levels[i].next.score < score ||
(x.levels[i].next.score == score && compareObj(robj, x.levels[i].next.robj))) {
x = x.levels[i].next
}
update[i] = x
}
2.3. 删除节点
删除节点就比较简单了，但是在这之前需要验证一下x指向的下一节点是不是需要删除的数据：
// x之后的节点可能是需要删除的节点，也可能不是
x = x.levels[0].next
if x != nil && x.score == score && equalObj(x.robj, robj) {
sl.deleteNode(update, x)
return true
}
在deleteNode中，进行如下删除步骤：
-
对每一层的update[i]进行：
-
- 如果update[i].levels[i]的下一节点是x，则进行x的删除，包括节点指针和span的改变
- 如果update[i].levels[i]的下一节点不是x，例如：删除s3节点，它的update[4].levels[4]下一节点是s4，此时直接将update[4].levels[4]的span减一
-
将x的next节点（如果有的话）挂在x的prev节点后面
-
更新跳表的level值。以删除s4节点为例，删除完该节点之后跳表实际层数应该调整为3。从第4层开始向下遍历，如果header.levels[i].next是nil，说明该层索引已经没必要存在了，就将跳表的level减一
-
别忘了把跳表的length减一
总结
跳表听起来挺难，如果仔细研究它的代码的话还是挺简单的。跳表主要难的地方就在于节点的插入和删除，只要理解了跳表的多级索引是怎么使用的，其他的操作：范围查询、查询排名等都比较简单了。这块的代码可以看redis的源码，在它的t_zset.c和redis.h中有zsl开头的代码就是跳表相关内容。不过我觉得更难的是写文档，写文档的时候需要阅读完代码之后理清思路，这块我发现通过画图还是可以加深理解的。