BNF范式

下面来自百度百科：

巴科斯范式（BNF）所描述的语法是与上下文无关的。它具有语法简单，表示明确，便于语法分析和编译的特点。

例：四则运算的BNF，<>表示非叶子节点，|表示或者关系，:=就是等于的意思。

<expr> ::= <expr> + <term>         | <expr> - <term>         | <term> <term> ::= <term> * <factor>         | <term> / <factor>         | <factor> <factor> ::= ( <expr> )           | Num

可见，BNF本质上就是树形分解，分解成一棵名为AST的抽象语法树。

产生式

BNF中的表达式叫做产生式。产生式就是将语法的分解规则表达出来的等式。如

句子 = 主 + 谓 + 宾

将语法规则用产生式描述出来是为了便于计算，产生式可以看作是对语法的数学建模。

产生式的特点是 不断向下分解。这种特点和数据结构中的树是一样的。
通过类比，有：

• 每个产生式就是一个子树，在写编译器时，每个子树对应一个解析函数。
• 叶子节点叫做 终结符，非叶子节点叫做 非终结符。

递归

产生式分成递归的和非递归的，如果一个产生式用自己来表示自己就会产生递归。
递归地调用自己的定义来定义自己，是无穷尽的。
比如：

• GNU项目的命名GUN NOT UNIX；
• A=A’b’（‘b’表示字符常量b）。

问：
明明代码文本都是有限长的，为什么还要引入递归这种模型来解析，搞得很复杂？

答：
实际的代码文本确实是有限长的。
但是，递归产生式只是定义了一个计算公式，通过这个计算公式，可以生成无穷种字符串。例如，四则运算可以用递归产生式来描述，它表示你可以写出无数个任意长的四则运算表达式，它是为了用一个公式来描述所有情况，是对实际规则的抽象与归纳。实际中，我们总不可能对每一种四则运算表达式都写一段解析代码，相反地，是所有四则运算表达式的解析都只用相同的解析程序。

递归又分为左递归和右递归，下面分别用图形的方式直观地进行描述。

左递归

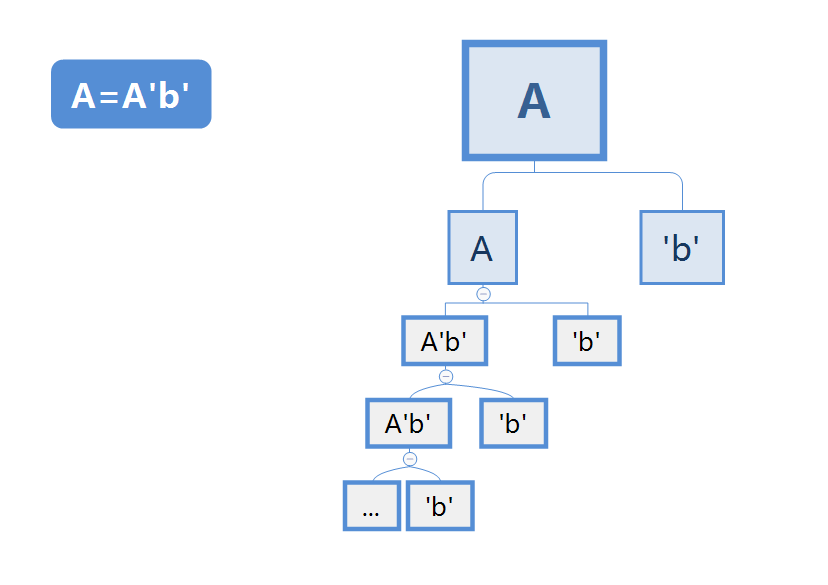
如上图所示，产生式一直朝左侧延伸，无法结束，永远不会结束，所以叫左递归。
显然左递归无法分解出有限的叶子节点。尤其是，它永远无法得到第一个叶子节点。因为左侧在无限递归产生新的左叶子节点。 这个结论很重要，要牢记。

右递归

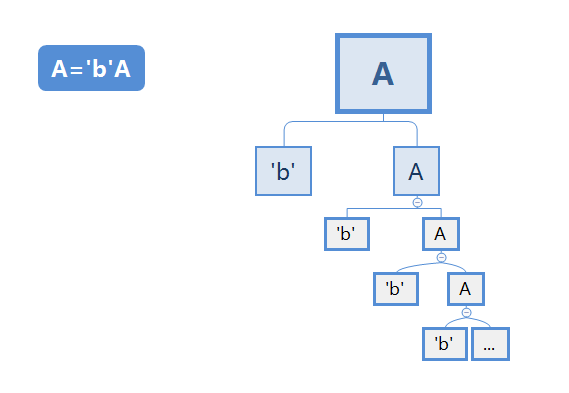
与左递归相反，右递归有第一个叶子节点，没有最后一个叶子节点。

如何判断产生式有递归？

示意图如下：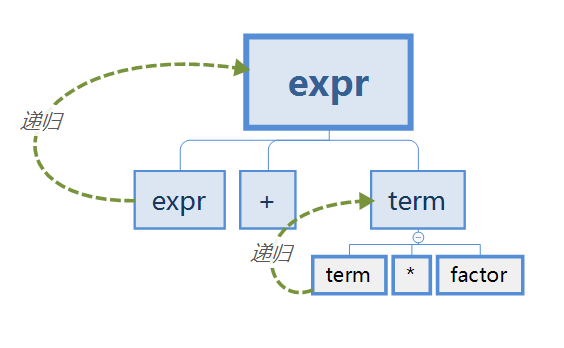
子节点和父节点相同叫直接左递归，子节点和非父节点的祖先相同叫间接左递归。

递归为什么可以消除？

因为某些左右递归可以相互转化，注意不是所有左右递归的都可以相互转化。具体是哪些呢，下面会说到，是包含终结符分支的递归表达式，终结符是转化的桥梁。

为什么只需要消除左递归？

我们需要明确第一个叶子节点的重要含义：第一个节点是语法的起点，所以第一个节点很重要，如果没有第一个叶子节点，那么就永远无法判断此语法是从哪个字符开始的。所以存在左递归的文法，是无法通过程序解析的，这样的程序无法实现。

相反地，右递归有第一个叶子节点，没有最后一个叶子节点。有第一个叶子节点就可以判断语法从哪个字符开始，但是不知道语法在何时结束。

但是，在实际解析中，因为被解析的文本是有限长的，所以右递归一定会停止。除此之外，因为右递归一定有起始符号，所以在解析文本时，一旦遇到非起始符的字符串，也会停止解析。也就是说，右递归能自动保证语法的正确性，而且不会无穷递归。

综上，只有左递归需要消除。

如何消除左递归

目前我们连产生式都不会写，怎么消除？所以接下来先把消除左递归的问题放一放，先弄清楚怎么编写产生式。

怎么编写产生式

要明确一个重要规则：优先级高的产生式必然是需要先被计算的。 所以优先级越高（如乘除运算）的产生式，在BNF树中越靠近叶子节点。优先级越低（如加减运算）的产生式，在BNF树中越靠近根节点。所以优先级低的产生式一定会被分解成优先级高的产生式。

另外，产生式中不可分解的元素一定是在叶子节点，叶子节点没有子节点，无法分解。

综上：

• BNF算法工作过程是，先向下分解到叶子节点，再从叶子节点沿着分解时的路径/调用堆栈向上反向计算。
• 产生式优先级和在BNF树中的深度成正比。
• 叶子节点有两种，一种是不可分解的元素，一种是优先级最高的元素。

以四则运算为例，双括号()的优先级最高，乘除运算*/的优先级其次，加减运算的优先级最低。从下面的四则运算的BNF可以看出，一个表达式是先分解成±运算，然后分解成乘除运算 */，最后再分解为Expr，这表明我们的理解是正确的。

<expr> ::= <expr> + <term>         | <expr> - <term>         | <term> 
<term> ::= <term> * <factor>         | <term> / <factor>         | <factor> 
<factor> ::= ( <expr> )           | Num

根据以上思想，下面具体描述产生式的编写过程。

四则运算表达式编写

问：

已知Expr支持形如5+3 * (2+1)的运算表达式，即支持运算优先级，乘除高于加减，支持括号括起来的子表达式。求产生式。

答：

• 5为Num，3为Num，(2 + 1)为含括号的子表达式(Expr)
• Num、(Expr)优先级最高，所以做叶子节点，把他们统称为Factor，即
  Factor=Num | (Expr)

• 次高优先级的运算为乘除运算*/，表达式称为Term，基本运算元素为上一步的Factor，有
  • 当乘除运算符个数为0时，Term = Factor
  • 当乘除运算符个数为1时，Term = Factor * Factor | Factor / Factor，将上式Term = Factor带入得 Term = Term * Factor | Term / Factor（左递归）。
  • 当乘除运算符个数大于1时，
    Term = Factor * Factor / Factor …* Factor = (Factor * Factor / Factor…) * Factor =Term * Factor
    或
    Term = Factor * Factor / Factor…/ Factor = (Factor * Factor / Factor…) / Factor = Term / Factor。
    于是运算符个数 >= 1时，具有相同产生式。综合得出：
    Term = Term * Factor | Term / Factor | Factor

• 最低优先级的运算为加减运算±，表达式称为Expr，基本运算元素为上一步的Term，有
  • 当加减运算符的个数为0时，Expr = Term
  • 当加减运算符的个数为1时，Expr = Term + Term | Term - Term，把上式代入得，
    Expr = Expr + Term | Expr - Term
  • 当加减运算符的个数大于1时，Expr = Term + Term - Term…+ Term = (Term + Term - Term…) + Term = Expr + Term，或 Expr = Term + Term - Term…- Term = (Term + Term - Term…) - Term = Expr - Term
    于是运算符个数 >= 1时，具有相同产生式。综合得出：
    Expr = Expr + Term | Expr - Term | Term

消除左递归

上面我们已经推导出四则运算的产生式了，但是产生式中存在之前说的左递归。具有左递归的产生式是无法用来解析代码的，所以需要消除左递归。
如何消除左递归呢？前面说过，用非递归的部分来表示左递归的部分就可以了。如果没有非递归部分，就无法消除左递归。就相当于一条路走不通，绕个弯子走另一条路。如果没有一条路可以走，就是真的无路可走。

消除直接左递归（省略号…表示无数次重复）：

现有直接左递归：A = Aa | b，
即A=A…a ，右边的A用b替换掉，等价于： A = ba…a = ba…
消除了左递归，即消除A =…a，只剩下A = ba…。
此时A的产生式为：A = bAtail，Atail是除了开始符号b剩下的部分。
那剩下的部分是什么呢？Atail = a…（右递归），即Atail = aAtail。右递归是可以处理的。
综上直接左递归消除方法是：
A = Aa | b =>消除左递归 => A = bA’， A’=aA’

由此可见，终结符是转化的桥梁。

消除间接左递归：

思路就是使用变量代换将间接左递归写成直接左递归，然后消除直接左递归。、